Your Ideal Math Lesson

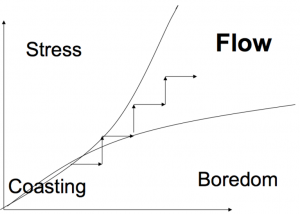I’ve been asking many of my grade 11 students what their ideal math lesson would look like.  Not in terms of content, but in terms of process.  I wanted to focus this question on math instead of science because I didn’t want to confound typical learning activities with demonstrations and experiments.

Most of the students cited very similar ideas, as follows:

  1. take up questions about homework or last day’s work
  2. connect the new material to what they were working on  last day
  3. possibly give some notes
  4. give (lots of) examples
  5. have them try some
  6. practice questions

#1 above was universal, all students started with this.  Irony: how many students try to finish homework, and how many are willing to ask a question?

#2 was interesting and makes a lot of sense.  This also agrees with the idea of checking with existing knowledge. This could take the form of an informal conversation, or doing something like have students fill out a KWL chart.

#3 was pretty common, but not universal.  Students don’t want to copy out a whole lot of notes. Several students said that if they are given full notes they may not pay attention to them, and that perhaps it’s best to have blanks to fill in (guided notes). I used to do all guided notes but started switching over to fully completed notes to save time. I’m not sure students really ever read notes to look for an explanation.  Peter Liljedhal says that something like 90% of students never look at their notes for studying (or learning presumably).  Perhaps an electronic notebook (OneNote) should be adopted, to save wasting paper. Of course there can be equity problems with OneNote.

#4, this was also universal.  I had to ask a lot of questions but it seems that students agree that they should be given the solution for the example as opposed to copying it.  There was some disagreement on whether if the teacher should work the solution from scratch on the board at the front.

#5 of course students expect to try some.  They like the idea of trying them right after a worked example is given.

#6, of course.

A few themes emerged from this.  First, much of what the students want can be tweaked into a set of procedures that should minimize cognitive load.  Second, there was general agreement that several, if not a majority of students, would not engage with 3, 4 and 5.  With 4 and 5, the question for me is how many students need to be engaged to make the task worthwhile?  25%? 50%? 75%?  I notice that when doing an example that there are many kids not listening but simply using their phones.  Furthermore, many people would agree that lots of students don’t “try one.”  Many students will simply wait for the teacher to give the answer, they’ll copy from their neighbour, or they’ll pretend to try.  One estimate, from Peter Liljedhal, says that perhaps only 28% of a class will authentically attempt the “now you try one.”  This certainly matches the estimations I made when I used to wait for students to “try one now.”  The secret to making this work is to use of effective formative assessment techniques during and after the “try one now.”  I don’t go over the solution, although I will post an answer.  I don’t give the students any reason to wait until something is done for them.

I think there is no doubt that much of the above flow can be worked into a good lesson or unit plan. I would adjust some of the tasks as required, in order to ensure that time is wisely spent.  For example, modeling a solution to the whole class when only 1/3 are paying attention is probably not worth it.  As well, much of physics 11 can be founded on modeling instruction, where paradigm labs, group work and Socratic discussion, and other interactive and interesting activities can take place.

If I asked my math 8 students what their ideal class looked like, it would be nothing like the above.  I’ve had a tremendous amount of positive feedback this year for math 8, where we have been centering our thinking around group work and interesting problems.  We can do this in math 8 because the content itself has very intuitive and foundational characteristics, which allows for “low-floor, high-ceiling” thinking.  We can start with an interesting problem because of the low floor.  This doesn’t meant that we don’t do worked examples or have any notes. We do, but those activities are typically quite short and don’t have to happen every day.