Fractions, Lesson 1

Research has long shown that fraction arithmetic is difficult for students. We also now know that success when working with fractions is one of the best predictors for success in post-secondary education. With this in mind, one of my prime focuses in math 8 is to do the very best I can with teaching fractions to my students.

The research on fraction arithmetic tells us that by grade 8, students have a success rate of around 50% when adding fractions. For some people in BC, this issue with fractional arithmetic is compounded by what they see as a weakness in the new BC Curriculum. In their minds, fraction arithmetic should start much earlier in the curriculum. In BC we start working on equivalent fractions in grade 5, but we don’t do any addition, subtraction or division until grade 8. The research on fractions and university success is used to convince people we should be starting earlier. The argument that we are falling behind other countries in standardized tests (Singapore, Japan, China?) is also used.

While I completely agree with the issues mentioned in my first paragraph, I strongly disagree with the opinions that I mention in the paragraph preceding this one.

Success with fractions is correlational to university success and has not been shown to be causational.
As far as I know, the early success with working with fractions is predictive because it is selective, not because actually knowing fraction arithmetic at a young age is in itself important for later success.
Research back in the 1980’s shows almost the exact same success rate with adding fractions in grade 8 as it does now. If starting fraction arithmetic earlier is better, we would expect to have more success in the 1980’s.
The concept of adding fractions should be simple. Kids can add numbers, and my experience is that kids are good at finding equivalent fractions.
Research done by Rober Siegler and others has emphasized the advantages of seeing fractions as numbers, rather than parts of a whole.
In terms of standardized test scores, I believe it’s impossible to say that Asian teaching methods are better. Any comparison needs to consider that their school systems incorporate many more instructional minutes and institutionalized tutoring.

Last year I focused on three aspects for adding and subtracting fractions. First was that fractions are numbers and numbers are easy to add. Second, fractions with the same bottom number (denominator) are really easy to add. Third, it’s pretty easy to find equivalent fractions and get fractions with the same bottom number.

Those are three basic understandings that are either self-evident or at least easy to remember. In terms of methods for adding fractions, we would simply use our existing skills and understandings (pre grade 8) and apply them to a new situation. I am very much against trying to have kids follow a prescribed algorithm because I believe it is unnecessary and evidently not successful. I used the word “prescribed” for a very deliberate reason. A basic intuitive approach to adding fractions based on two principles (numbers are easy to add, and fractions are easy to add when they have the same denominator) is the same as the algorithm, but presented in a conceptually understandable way.

The last piece in the puzzle for success in fraction arithmetic is taking advantage of some general teaching methods. We should incorporate spaced practice (practice adding fractions over a period of time) and we should interleave the practice.

With the above ideas in place, I think it’s easily achievable to have well over 80% of a grade 8 math class correctly answer fractional arithmetic questions on pop quizzes.

Lesson 1

The lesson starts with me tying a piece of string across the classroom.

“Mr. Smith, why are you putting up that string?” “I have some wet clothes to dry.” Hey, days are long when you’re a teacher. Humour helps.

Everyone knows what a number line is, right? Have a short discussion with your neighbour and come up with some properties of number lines.

Ok, ready? I’ll pick people at random to tell me a property.

- they’re usually straight lines. “Good! straightish is nice, but they can probably be curved too” (my clothesline is curved!).

- integers and numbers go on them

- you put dash lines on the number line. “What do you know about the spacing of the dashes?”

- the dashes are evenly spaced

Alright, everyone now has to come up here and grab a piece of paper from my and a clip. Now that you have your paper, you’ll see that everyone has a number. I want you to clip your number on the string. You’ll have to work with your peers to figure out where your number should go.

<5 - 10 minutes pass as kids place their numbers, argue, move numbers, etc. This is the easy 10 min of my day.>

Alright, let’s all look at the number line. Does anyone see any mistakes? Is there anything we could improve?

Fantastic. Looks good. There is one huge lesson to learn from this. Fractions are numbers. We can take a fraction and put it in an exact position on a number line, just like a natural number or integer. It doesn’t matter if it is a part, a whole, a mixed fraction, whatever. Fractions are numbers.

Back your desks please. Now take a look at these four numbers. Talk with your neighbour and decide Which One Doesn’t Belong, and why it doesn’t belong. I’ll randomly pick someone to tell me what they think.

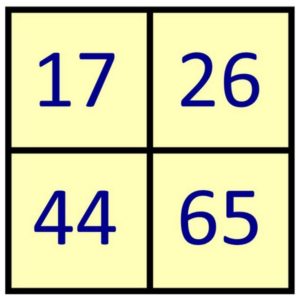
- 17, it’s the only prime number

- 44, it’s the only one that has the same two digits

- 65 because the other ones have their digits add up to 8 (1+7, 2+6, 4+4) [my favorite answer!]

Ok, now let’s try a couple of ones with fractions

So you already practiced ordering fractions on a number line. I know have a series of questions I’d like you to work on with the whiteboards. I want you to identify which one is greater.

Take a look around the room. It looks like most of you agree on your answers. There is one that is quite different though. Which is it?

- 3/8 or 4/10.

Who can explain why they think 3/8 is bigger?

- I know that 1/8 is bigger than 1/10 and since 3 is only 1 smaller than 4 and the 8 is bigger, I think 3/8 is bigger

Who can explain why they think 4/10 is bigger?

- We found some equivalent fractions. If we times the 4 and 10 by 4 we get 16/40, and if we times the 3 and 8 by 5 we get 15/40. 16/40 is bigger than 15/40

That sounds pretty convincing to me! Ok, everyone needs to go back to their seats. What I want you to do is to write down one or two things that you learned today, or things that you had forgotten and now remember about fractions.