Dialogue in a Thinking Classroom

I’ve seen lots of pictures of math Thinking Classrooms on twitter and I’ve also come across a few videos.  I haven’t seen anything that followed the dialogue in a classroom, so I thought I’d try to capture a bit of that aspect in this blog post.  What I have below isn’t all that different from a lot of lessons except that you have to visualize how the students are situated.  They are not copying something down from me.  They have to write everything themselves and chances are that at some point they will have to justify what they’re doing to the others in their group.  The topic for today was adding integers.

OK, I’ve put everyone in their random groups.  Remember, one pen per group and switch the pen after every question.

On your whiteboard, write down the sum of 5 + (-2) . Use a number line to show your reasoning.
Now try 5 + (-7)
Now try (-1) + (-4)

<kids worked pretty fast, about 1/2 needed number lines> Let’s see what everyone did… what pattern do you see? Is there a rule that you can use?

- Adding a negative makes the number negative?
- Adding a negative number makes the number smaller?

What about (-1) + (-4)? Is the (-1) getting bigger or smaller?
What does this look like with money?

- If you owe someone a dollar and then owe them 4 more dollars, then you owe them more money. So adding a negative number is like increasing how much money you owe them.

Yes, in all cases the number is becoming more negative. Let’s go back to your seats and write down that rule in your own words.

Ok, try these Suduko type puzzles: Integers Two Ways

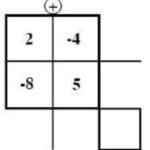
<lots of success, some good arguments and collaboration around solving the puzzles, making corrections, sharing>

- can we use a number line?  You bet you can.
- Mr. Smith, we’re done

If you’re finished, make your own puzzle.

Ok everyone, I just gave you a piece of paper. Put your name on it and try the three puzzles that your classmates made. Individual work and hand it in to me when you’re finished so I can see how you’re doing.

Last thing today. Who can add 48234 + (-1454) in their head in less than 2 seconds? Who can add 4534 + (-340823) in less than 2 seconds?

<lots of head scratching, no one can do it quickly>

What about 9932 + (-9932) ? Why is that so easy?

- Because they’re opposites, they cancel each other out

Yes, they are opposites. Opposites add together to 0. We call them additive inverses but opposites is easier to say. We’ll talk more about them in the days ahead.